|
Cardioid
|
Med
Lrg
|
|
Description :
|
The cardioid is the path followed by a point on the
circumference of a circle of radius one unit as it rolls around the
circumference of another circle of radius one unit.
It is formed here from its tangents by laying N points equally on a
circle, and joining point n to the point (2n + N/2) mod N.
|
|
|
 |
| |
|
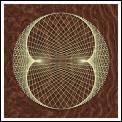
Nephroid
|
Med
Lrg
|
|
Description :
|
The nephroid is the path followed by a point on the
circumference of a circle of radius one unit as it rolls around the
circumference of a circle of radius two units.
It is formed here from its tangents by laying N points equally on a
circle, and joining point n to the point (3n + N/2) mod N.
|
|
|
 |
| |
|
Epicycloid 1:3
|
Med
Lrg
|
|
Description :
|
The curve is the path followed by a point on the
circumference of a circle of radius one unit as it rolls around the
circumference of a circle of radius three units.
It is formed here from its tangents by laying N points equally on a
circle, and joining point n to the point (4n + N/2) mod N.
|
|
|
 |
| |
|
Epicycloid 1:4
|
Med
Lrg
|
|
Description :
|
The curve is the path followed by a point on the
circumference of a circle of radius one unit as it rolls around the
circumference of a circle of radius four units.
It is formed here from its tangents by laying N points equally on a
circle, and joining point n to the point (5n + N/2) mod N.
|
|
|
 |
| |
|
Epicycloid 1:5
|
Med
Lrg
|
|
Description :
|
The curve is the path followed by a point on the
circumference of a circle of radius one unit as it rolls around the
circumference of a circle of radius five units.
It is formed here from its tangents by laying N points equally on a
circle, and joining point n to the point (6n + N/2) mod N.
|
|
|
 |
| |
|
Epicycloid 1:6
|
Med
Lrg
|
|
Description :
|
The curve is the path followed by a point on the
circumference of a circle of radius one unit as it rolls around the
circumference of a circle of radius six units.
It is formed here from its tangents by laying N points equally on a
circle, and joining point n to the point (7n + N/2) mod N.
|
|
|
 |
| |
|
Epicycloid 1:8
|
Med
Lrg
|
|
Description :
|
The curve is the path followed by a point on the
circumference of a circle of radius one unit as it rolls around the
circumference of a circle of radius eight units.
It is formed here from its tangents by laying N points equally on a
circle, and joining point n to the point (9n + N/2) mod N.
|
|
|
 |
| |
|
Epicycloid 1:12
|
Med
Lrg
|
|
Description :
|
The curve is the path followed by a point on the
circumference of a circle of radius one unit as it rolls around the
circumference of a circle of radius twelve units.
It is formed here from its tangents by laying N points equally on a
circle, and joining point n to the point (13n + N/2) mod N.
|
|
|
 |
| |
|
Astroid
|
Med
Lrg
|
|
Description :
|
The astroid is the path followed by a point on the
circumference of a circle of radius one unit as it rolls inside the
circumference of a circle of radius four units.
It is formed here from its tangents by choosing a length L
and then joining points on the x-axis to points at distance L on the
y-axis. All the tangent strings in the image have length L.
|
|
|
 |
| |
|
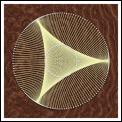
Deltoid
|
Med
Lrg
|
|
Description :
|
The deltoid is the path followed by a point on the
circumference of a circle of radius one unit as it rolls inside the
circumference of a circle of radius three units.
It is formed here from its tangents by laying N points equally on a
circle (the inner circle), and joining point n to the point (N/2 - 2n) mod N.
The strings are extended to an outer circle whose radius is 3 times
the inner circle radius.
|
|
|
 |
| |
|
Astroid
|
Med
Lrg
|
|
Description :
|
The astroid is the path followed by a point on the
circumference of a circle of radius one unit as it rolls inside the
circumference of a circle of radius four units.
It is formed here from its tangents by laying N points equally on a
circle (the inner circle), and joining point n to the point (N/2 - 3n) mod N.
The strings are extended to an outer circle whose radius is 2 times
the inner circle radius.
|
|
|
 |
| |
|
Hypocycloid 1:5
|
Med
Lrg
|
|
Description :
|
The curve is the path followed by a point on the
circumference of a circle of radius one unit as it rolls inside the
circumference of a circle of radius five units.
It is formed here from its tangents by laying N points equally on a
circle (the inner circle), and joining point n to the point (N/2 - 4n) mod N.
The strings are extended to an outer circle whose radius is 5/3 times
the inner circle radius.
|
|
|
 |
| |
|
Hypocycloid 1:6
|
Med
Lrg
|
|
Description :
|
The curve is the path followed by a point on the
circumference of a circle of radius one unit as it rolls inside the
circumference of a circle of radius six units.
It is formed here from its tangents by laying N points equally on a
circle (the inner circle), and joining point n to the point (N/2 - 5n) mod N.
The strings are extended to an outer circle whose radius is 3/2 times
the inner circle radius.
|
|
|
 |
| |
|
Hypocycloid 1:8
|
Med
Lrg
|
|
Description :
|
The curve is the path followed by a point on the
circumference of a circle of radius one unit as it rolls inside the
circumference of a circle of radius eight units.
It is formed here from its tangents by laying N points equally on a
circle (the inner circle), and joining point n to the point (N/2 - 7n) mod N.
The strings are extended to an outer circle whose radius is 4/3 times
the inner circle radius.
|
|
|
 |
| |
|
Hypocycloid 1:12
|
Med
Lrg
|
|
Description :
|
The curve is the path followed by a point on the
circumference of a circle of radius one unit as it rolls inside the
circumference of a circle of radius twelve units.
It is formed here from its tangents by laying N points equally on a
circle (the inner circle), and joining point n to the point (N/2 - 11n) mod N.
The strings are extended to an outer circle whose radius is 6/5 times
the inner circle radius.
|
|
|
 |
| |
