|
|
 |
|
|
|
| |
Several programs have features involving symmetry:
- antiview, off2vrml, off2pov -
display symmetry elements
- poly_kscope -
repeats a model symmetrically, used to make compounds
- off_align -
repeats a model symmetrically, used to augment polyhedra
- off_trans -
aligns a model according to symmetry
- off_report -
prints symmetry information for a model
- off_color -
colours by symmetry orbit
The program option parameters are organised around the following ideas
- Symmetry group
- A set of (Euclidean) transformations that carry a
polyhedron onto itself, described in general form using
Schoenflies notation (see below) e.g. Oh, D3v.
- Full symmetry group of a polyhedron
- The set of all (Euclidean) transformations that carry a
polyhedron onto itself.
- Symmetry subgroup, or subsymmetry
- A set of transformations from a symmetry group which, considered
alone, also form a symmetry group, e.g. a cube has Oh symmetry
and has a 3-fold axis corresponding to a C3v subgroup.
- Symmetry orbit of an element
- A set of equivalent elements, those elements that this element is
carried on to by a symmetry or subsymmetry of the model.
- Standard alignment of a symmetry
- A symmetry group could be aligned anywhere in the coordinate
system, but there are particular alignments that fit nicely
with the coordinate axes, and these are used as the 'standard'
alignments in Antiprism. They are a way of associating a symbol
like D3v with a fixed set of transformations.
- Conjugation subtype of a subsymmetry
- This is an integer used to distinguish subgroups which are
not carried onto each other (by conjugation) by the
transformations of the parent symmetry group. For example a
cube has a 2 fold axis through mid-edge and a 2-fold axis
through a face centre. There is no symmetry of the cube that
carries one onto the other and so they will have different
subtype numbers. Geometrically, they look different in the cube.
- Symmetry realignment
- If you align a polyhedron with the standard set of symmetries
for its full symmetry group there is often more than one
distinct way to achieve this (a transformation not in
the symmetry group that transforms the symmetry group onto
itself). For example, if you align a cereal box-like cuboid
naturally with the coordinate axes there are 6 possibilities
i.e. the centres of the three rectangle types can lie on any
of the axes, with 3x2x1 = 6. Possibilities for some polyhedra
are infinite e.g. the symmetry group of a pyramid does not change
when it is translated along its principal axis. The realignment
is given by a series of colon separated numbers, the first
number selects from a finite set of realignments, and the
following numbers are decimals to control rotations and
translations as follows:
- axial rotation:
1 number - degrees around principle axis
- full rotation:
3 numbers - degrees around x, y and z axes
- axial translation:i
1 number - distance to translate along principal axis
- plane translation:
2 numbers - distance to translate along two
orthogonal directions in (mirror) plane
- full translation:
3 numbers - distance to translate along x, y and z axes
- Schoenflies notation
- Used to specify symmetry groups. The standard alignments have,
preferentially, a centre (fixed point) on the origin a principal
rotational axes on the z-axis, a dihedral axis on the x-axis, a
mirror normal on the y-axis (except Cs has a mirror normal on the
z-axis). The polyhedral symmetry types have a 3-fold axis on (1,1,1).
In the following list of symbols, when a type contains 'n' this must
be replaced by an integer (giving an n-fold axis), and for S this
integer must be even.
- C1 - identity
- Cs - mirror
- Ci - inversion
- Cn - cyclic rotational
- Cnv - cyclic rotational with vertical mirror
- Cnh - cyclic rotational with horizontal mirror
- Dn - dihedral rotational
- Dnv - dihedral rotational with vertical mirror
- Dnh - dihedral rotational with horizontal mirror
- Sn - cyclic rotational (n/2-fold) with rotation-reflection
- T - tetrahedral rotational
- Td - full tetrahedral
- Th - tetrahedral with inversion (pyritohedral)
- O - octahedral rotational
- Oh - full octahedral
- I - icosahedral rotational
- Ih - full icosahedral
There are two symmetry reports. off_report -S s gives a general listing
of the full symmetry, subsymmetries with numer of types, realignment
possibilities and the axes with their number
off_report -S s rh_cubo
The subsymmetry and realignment possibilities indicate what will be
valid in the symmetry options.
There is also a list of orbits, with the total number of orbits for
each element type, and the number of elements in each orbit.
off_report -C O rh_cubo
A value of 1 for verts, edges, faces indicates the polyhedron is
repsepctively isogonal, isotoxal, isohedral.
The orbits can also be calculated for a subgroup, using the
-y option
off_report -y D2h -C O rh_cubo
off_report -y D2h,1 -C O rh_cubo
These are the same orbits that are used for colouring.
The first
number indicates the number of colours that will be used, and the
second numbers are the number of elements having each colour
off_color -f S rh_cubo | antiview
off_color -f S,D2h rh_cubo | antiview
off_color -f S,D2h,1 rh_cubo | antiview
|
|
| |
|
|
| |
|
View symmetry
|
Med
Lrg
|
|
Description :
|
antiview, off2pov and off2vrml can display
symmetry elements using the -s option. The axes (x), mirror
planes (m) and rotation reflection planes (r) can be viewed
independently and in combination. View them all with -s a,
as in the example command. antiview can also cycle through
the display of symmetry elements by pressing y while viewing a
model.
View this model with the command
off_trans -R 0,20,0 -R 15,0,0 cube | antiview -s a
|
|
|
 |
| |
|
Kaleidoscope
|
Med
Lrg
|
|
Description :
|
poly_kscope repeats a model symetrically, acting like a
polyhedral kaleidoscope. Only one example is included here, there
are more in the
poly_kscope examples album.
When making a compound the component will generally have
symmetries that are also symmetries of the compound. It
could be difficult to align a component into a position
where symmetries are shared using rotations and
translations, as an alternative there is a facility to do
this directly by symmetry. The option -y list will list
all arrangements of the component and final symmetry
according to how the component can be aligned to share
a common symmetry group with the kaleidoscope. To make the
model rerun the command but replace 'list' with the number
and any optional realignment. Running this for the previous
cube example, produces a list with 20 items
poly_kscope cube -s Ih -y list
The last number is 19 and corresponds to the compound of
5 cubes, as in the previous example
poly_kscope cube -s Ih -y 19 | antiview
In the following example the cube will be aligned on a
C3v axis, and the optional realignment translates the
cube 2 units along the icosahedral 3-fold axis.
View this model with the command
poly_kscope cube -m f,compound -s Ih -y 8,:2 | antiview -v 0.05
|
|
|
 |
| |
|
Excavate Full
|
Med
Lrg
|
|
Description :
|
The -F option of off_align aligns a face on the
brick with a face on the base
and then uses it to augment or excavate the base model (the polyhedra
are joined and the bonding faces removed). This operation can be
repeated symmetrically with the -y option.
In this example the base polygon of a pentagonal
pyramid is aligned with a face of a dodecahedron. An alignment
number is chosen that causes the pyramid to lie inside the dodecahedron,
producing an excavation. The bonding operation is repeated with the
symmetry of the base model by specifying -y full.
View this model with the command
off_align -F pyr5,0,0,5 -y full dodecahedron | antiview
|
|
|
 |
| |
|
Augment Full
|
Med
Lrg
|
|
Description :
|
The -F option of off_align aligns a face on the
brick with a face on the base
and then uses it to augment or excavate the base model (the polyhedra
are joined and the bonding faces removed). This operation can be
repeated symmetrically with the -y option.
In this example a tetrahedron is aligned with a face of an icosahedron.
The default alignment causes the tetrahedron to lie outside the
icosahedron, producing an augmentation.
The bonding operation is repeated with the
symmetry of the base model by specifying -y full.
View this model with the command
off_align -F tet -y full icosahedron | antiview
|
|
|
 |
| |
|
Augment Subsym
|
Med
Lrg
|
|
Description :
|
The -F option of off_align aligns a face on the
brick with a face on the base
and then uses it to augment or excavate the base model (the polyhedra
are joined and the bonding faces removed). This operation can be
repeated symmetrically with the -y option.
In this example a triangular prism is aligned with a face of an icosahedron.
The bonding operation is repeated with tetrahedral symmetry, a subsymmetry
of the base model, by specifying -y T.
View this model with the command
off_align -F pri3,5 -y T icosahedron | antiview
|
|
|
 |
| |
|
Align full
|
Med
Lrg
|
|
Description :
|
Align a cube with the standard symmetry for its full symmetry. The
square prism model, pri4, is a cube, but by construction is
not aligned with the standard octahedral axes. This command shows
how any model can be aligned with its standard symmetry group.
View this model with the command
off_trans -y full pri4 | antiview
|
|
|
 |
| |
|
Align sub 0
|
Med
Lrg
|
|
Description :
|
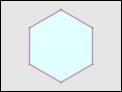
Align the first C3v subgroup (subtype 0) of a hexagonal pyramid with
the standard C3v symmetry
View this model with the command
polygon pyr 6 | off_trans -y C3v | antiview
|
|
|
 |
| |
|
Align sub 1
|
Med
Lrg
|
|
Description :
|
The hexagonal pyramid has two C3v subgroups, align the second C3v
subgroup (subtype 1) of a hexagonal pyramid with the standard C3v
symmetry
View this model with the command
polygon pyr 6 | off_trans -y C3v,1 | antiview
|
|
|
 |
| |
|
Align sub 1 2
|
Med
Lrg
|
|
Description :
|
Align the second C3v subgroup (subtype 1) of a hexagonal pyramid
with the standard C3v symmetry. Then select an alternative
alignment for this group using the third specifier, in this
case realignment 2.
View this model with the command
polygon pyr 6 | off_trans -y C3v,1,2 | antiview
|
|
|
 |
| |
|
Align cuboid
|
Med
Lrg
|
|
Description :
|
There are six ways to align a cuboid with its full symmetry group.
Rerun the command with the last number running from 0 to 5 to
see all the alternatives.
View this model with the command
off_trans cube -S 1,2,3 | off_trans -y full,0,0 | antiview
|
|
|
 |
| |
|
Align with poly
|
Med
Lrg
|
|
Description :
|
Aligning one polyhedron with another is a two stage process. The
polyhedron to be aligned is aligned with a standard symmetry using
the -y option. The standard symmetry is then aligned with a subgroup
of the same type in the fixed polyhedron using the -Y option.
In this case, a C3v subgroup of a hexagonal pyramid is aligned with
a C3v subgroup of a cube.
View this model with the command
polygon pyr 6 | off_trans -y C3v -Y cube,C3v | antiview - cube
|
|
|
 |
| |
|
Align with poly
|
Med
Lrg
|
|
Description :
|
The cube only has one type of C3v subgroup but the hexagonal
pyramid has two. In this example a C3v subgroup of a hexagonal
pyramid is aligned with a C3v subgroup of a cube again, but
a second alignment is specified.
View this model with the command
polygon pyr 6 | off_trans -y C3v,1 -Y cube,C3v | antiview - cube
|
|
|
 |
| |
|
Align with poly
|
Med
Lrg
|
|
Description :
|
Realignments also work when aligning one polyhedron with another,
and may be applied using either the -y or -Y option.
In this case, a C3v subgroup of a hexagonal pyramid is aligned with
a C3v subgroup of a cube, which is followed by a realignment by
translating along the principal axis
View this model with the command
polygon pyr 6 | off_trans -y C3v -Y cube,C3v,0,0:-1.0 | antiview - cube
|
|
|
 |
| |
|
Align with poly
|
Med
Lrg
|
|
Description :
|
When aligning one polyhedron with another, sometimes the fixed
symmetry will have more than one type of the subsymmetry.
Select between them with the third part of option -Y.
In this case, a cuboid is aligned on the second kind of D2h
group of a cube (specified with the number 1).
View this model with the command
off_trans cube -S 0.5,1.5,3 | off_trans -y full -Y cube,D2h,1 | antiview - cube
|
|
|
 |
| |
|
Align with sym
|
Med
Lrg
|
|
Description :
|
The -Y option will also work with a standard symmetry type, which
will create an alignment suitable for use with poly_kscope. However,
poly_kscope also includes support for this through its own -y
option.
This example makes uniform compound UC40, consisting of 6 decagonal
prisms
View this model with the command
off_trans -y D5v,1 -Y Ih,D5v pri10 | poly_kscope -s Ih -c f -m compound | antiview
|
|
|
 |
| |
|
Colour Full
|
Med
Lrg
|
|
Description :
|
A symmetrical colouring can be made by colouring the elements
according to symmetry orbits.
In this example, the square faces of the rhombicuboctahedron
fall into two orbits under
the full symmetry of the model (faces on 4-fold axes and faces
on 2-fold axes). The following command assigns different colours
to the different kinds of face.
View this model with the command
off_color -f S rh_cubo | antiview
|
|
|
 |
| |
|
Colour Sub0
|
Med
Lrg
|
|
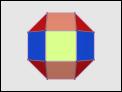
Description :
|
A symmetrical colouring can be made by colouring the elements
according to symmetry orbits.
In this example, the square faces of the rhombicuboctahedron
fall into six orbits under the default D2h sub-symmetry of the model.
The following command assigns different colours
to the different kinds of face.
View this model with the command
off_color -f S,D2h rh_cubo | antiview
|
|
|
 |
| |
|
Colour Sub1
|
Med
Lrg
|
|
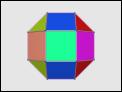
Description :
|
A symmetrical colouring can be made by colouring the elements
according to symmetry orbits.
In this example, the square faces of the rhombicuboctahedron
fall into five orbits under the second D2h sub-symmetry (specified
as subsymmetry number 1) of the model.
The following command assigns different colours
to the different kinds of face.
View this model with the command
off_color -f S,D2h,1 rh_cubo | antiview
|
|
|
 |
| |
|
|
|
|
|
Home
|
Programs
|
Examples
|
Album
|
Download
|
Development
|
Forum
|
About
|
